Metric Graph Reconstruction from Noisy Data
| IJCGA: | International Journal of Computational Geometry and Applications, pages 305-325, 2012. |
| SoCG'11: | Proceedings of the Annual Symposium on Computational Geometry, pages 37-46, 2011. |

|
IJCGA |

|
SoCG'11 |
| DOI: | 10.1142/S0218195912600072 |
Abstract
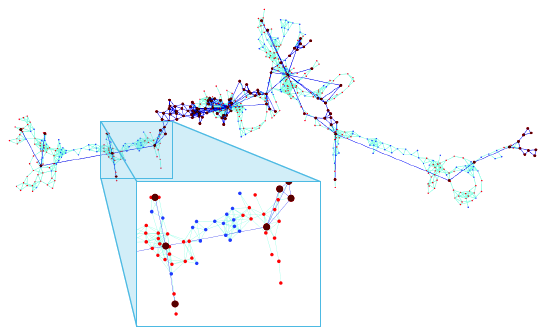
Many real-world data sets can be viewed of as noisy samples of special types of metric spaces called metric graphs [16]. Building on the notions of correspondence and Gromov-Hausdorff distance in metric geometry, we describe a model for such data sets as an approximation of an underlying metric graph. We present a novel algorithm that takes as an input such a data set, and outputs the underlying metric graph with guarantees. We also implement the algorithm, and evaluate its performance on a variety of real world data sets.
Many real-world data sets can be viewed of as noisy samples of special types of metric spaces called metric graphs [16]. Building on the notions of correspondence and Gromov-Hausdorff distance in metric geometry, we describe a model for such data sets as an approximation of an underlying metric graph. We present a novel algorithm that takes as an input such a data set, and outputs the underlying metric graph with guarantees. We also implement the algorithm, and evaluate its performance on a variety of real world data sets.