The Robustness of Level Sets
| Proceedings of the 18th Annnual European Symposium on Algorithms, Lecture Notes in Computer Science 6346, 1-10, 2010. |

|
ESA |
Update: The full version of this paper is Homology and Robustness of Level and Interlevel Sets.
Abstract
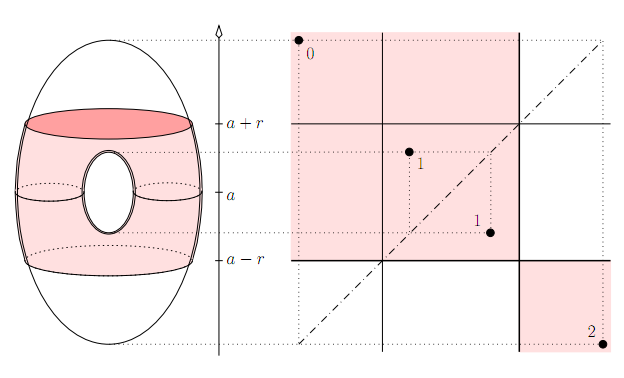
We define the robustness of a level set homology class of a function f: X → R as the magnitude of a perturbation necessary to kill the class. Casting this notion into a group theoretic framework, we compute the robustness for each class, using a connection to extended persistent homology. The special case X = R3 has ramifications in medical imaging and scientific visualization.
We define the robustness of a level set homology class of a function f: X → R as the magnitude of a perturbation necessary to kill the class. Casting this notion into a group theoretic framework, we compute the robustness for each class, using a connection to extended persistent homology. The special case X = R3 has ramifications in medical imaging and scientific visualization.
References
[3]
Gunnar Carlsson, Vin de Silva, and Dmitriy Morozov. Zigzag persistent homology and real-valued functions. Proceedings of the Annual Symposium on Computational Geometry, pages 247–256, 2009.
[8]
Herbert Edelsbrunner, Dmitriy Morozov, and Amit Patel. Quantifying transversality by measuring the robustness of intersections. Manuscript, Deptartment of Computer Science, Duke University, Durham, North Carolina, 2009.