Inferring Local Homology from Sampled Stratified Spaces
| Proceedings of the 48th Annual IEEE Symposium on Foundations of Computer Science, pages 536-546, 2007. |

|
Full version |
| Official IEEE version: | through IEEEXplore |
Abstract
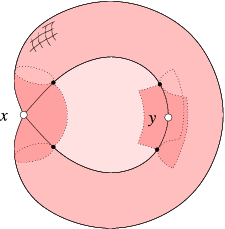
We study the reconstruction of a stratified space from a possibly noisy point sample. Specifically, we use the vineyard of the distance function restricted to a 1-parameter family of neighborhoods of a point to assess the local homology of the stratified space at that point. We prove the correctness of this assessment under the assumption of a sufficiently dense sample. We also give an algorithm that constructs the vineyard and makes the local assessment in time at most cubic in the size of the Delaunay triangulation of the point sample.
We study the reconstruction of a stratified space from a possibly noisy point sample. Specifically, we use the vineyard of the distance function restricted to a 1-parameter family of neighborhoods of a point to assess the local homology of the stratified space at that point. We prove the correctness of this assessment under the assumption of a sufficiently dense sample. We also give an algorithm that constructs the vineyard and makes the local assessment in time at most cubic in the size of the Delaunay triangulation of the point sample.
References
[6]
David Cohen-Steiner, Herbert Edelsbrunner and John Harer. Stability of persistence diagrams. In "Proc. 21st Ann. Sympos. Comput. Geom., 2005", 263-271.
[8]
David Cohen-Steiner, Herbert Edelsbrunner and Dmitriy Morozov. Vines and vineyards by updating persistence in linear time. Proceedings of the 22nd Annual ACM Symposium on Computational Geometry, pages 119-126, New York, NY, USA, 2006.
[12]
Herbert Edelsbrunner, David Letscher and Afra Zomorodian. Topological persistence and simplification. Discrete Comput. Geom. 28 (2002), 511-533.