Persistence-Sensitive Simplification of Functions on 2-Manifolds
| Proceedings of the Annual ACM Symposium on Computational Geometry, pages 127-134, 2006. |

|
SoCG'06 |
| Official ACM version: | through ACM portal |
Abstract
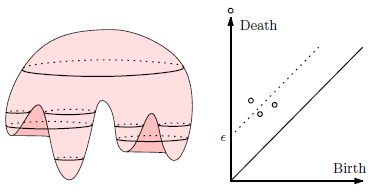
We continue the study of topological persistence [5] by investigating the problem of simplifying a function f in a way that removes topological noise as determined by its persistence diagram [2]. To state our results, we call a function g an ε-simplification of another function f if ||f - g||∞ ≤ ε, and the persistence diagrams of g are the same as those of f except all points within L1-distance at most ε from the diagonal have been removed. We prove that for functions f on a 2-manifold such ε-simplification exists, and we give an algorithm to construct them in the piecewise linear case.
We continue the study of topological persistence [5] by investigating the problem of simplifying a function f in a way that removes topological noise as determined by its persistence diagram [2]. To state our results, we call a function g an ε-simplification of another function f if ||f - g||∞ ≤ ε, and the persistence diagrams of g are the same as those of f except all points within L1-distance at most ε from the diagonal have been removed. We prove that for functions f on a 2-manifold such ε-simplification exists, and we give an algorithm to construct them in the piecewise linear case.
References
[2]
David Cohen-Steiner, Herbert Edelsbrunner and John Harer. Stability of persistence diagrams. In "Proc. 21st Ann. Sympos. Comput. Geom., 2005", 263-271.
[3]
Herbert Edelsbrunner, Valerio Pascucci, and Dmitriy Morozov. Persistence-Sensitive Simplification of Functions on 2-Manifolds. Proceedings of the Annual Symposium on Computational Geometry, pages 127-134, New York, New York, June 2006.
[5]
Herbert Edelsbrunner, David Letscher and Afra Zomorodian. Topological persistence and simplification. Discrete Comput. Geom. 28 (2002), 511-533.